Table of Contents

Graph

So we are given a line, and we are told the centre of a sphere. We are asked to find the radius of the sphere where:

  1. The sphere intersects the line twice.
  2. The sphere intersects the line once.
  3. The sphere does not intersect the line.

An example diagram is below.

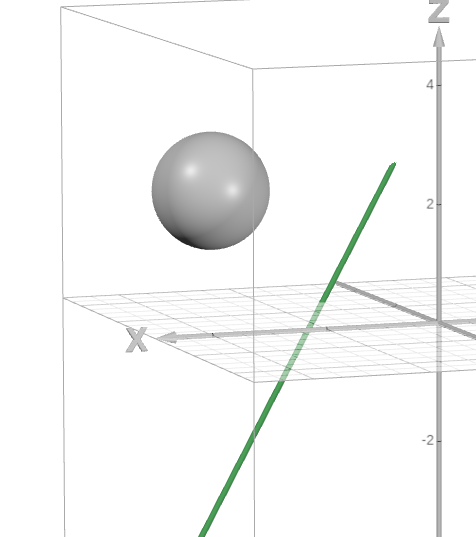
sphere line.png

Notice that when the sphere touches the line once, the line is tangential, and thus the radius is at $90°$ to the line.

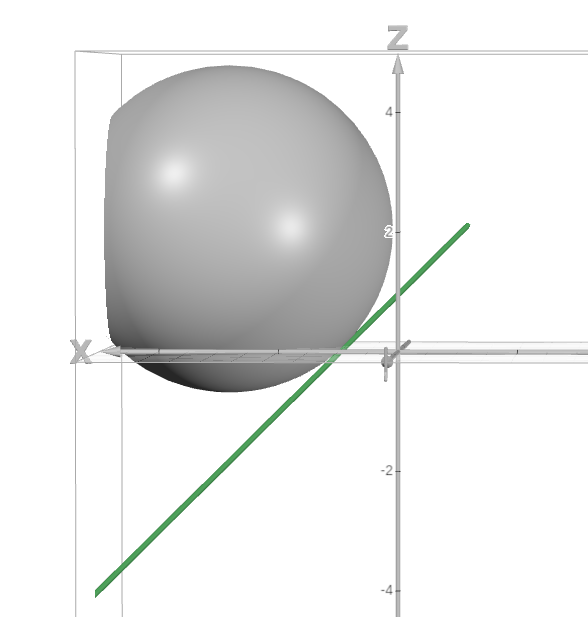
sphere line 2.png

But additionally, consider just the centre of the sphere in relation to the line.

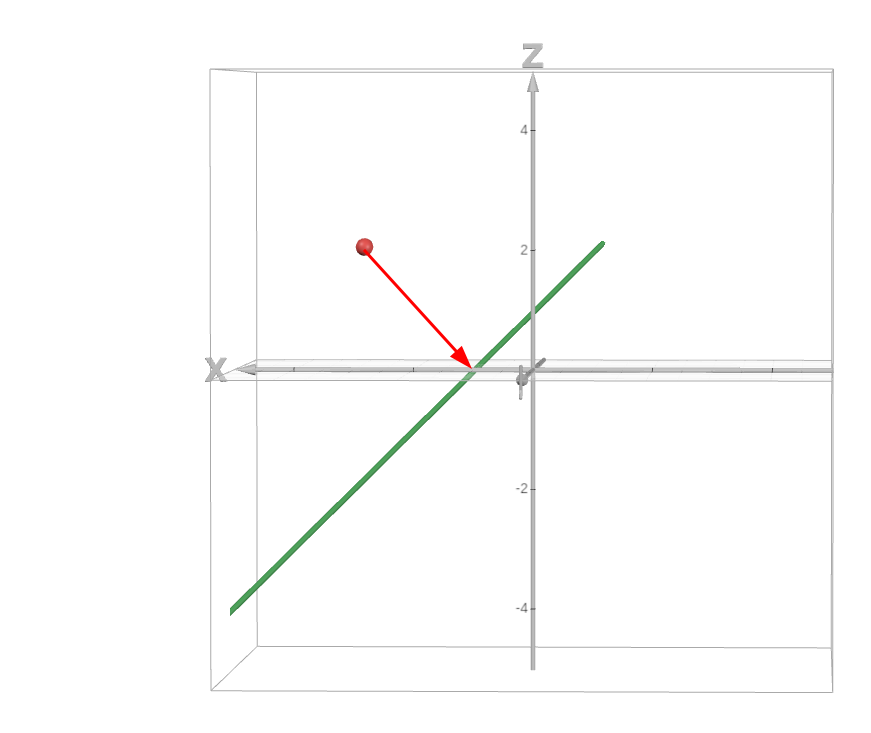
sphere line 3.png

This looks awfully similar to finding the minimum distance between a point and a line.

That's because it is!

Likewise how we may initially approach this by using the fact that the radius is perpendicular to the line, we use similar reasoning when finding the minimum distance between a point and a line.

Hence, given the following information:

$$\begin{align} L_{1}: & \ r= \begin{pmatrix}x_{1} \\ y_{1} \\ z_{1} \end{pmatrix} + \lambda\begin{pmatrix}x_{2} \\ y_{2} \\ z_{2} \end{pmatrix} \\ S_{1}: & \ \mid r-\begin{pmatrix}x_{3} \\ y_{3} \\ z_{3} \end{pmatrix} \mid = \alpha \end{align} $$

Then we can do the following:

  1. Find distance vector between point on $L_{1}$ and the centre of $S_{1}$
$$\begin{align} \vec{d}=\begin{pmatrix}x_{1} + \lambda x_{2} -x_{3}\\ y_{1} + \lambda y_{2} -y_{3} \\ z_{1} + \lambda z_{2} -z_{3} \end{pmatrix} \end{align} $$
  1. Equate dot product of $\vec{d}$ and $\begin{pmatrix}x_{2} \ y_{2} \ z_{2} \end{pmatrix}$ to 0 to solve for $\lambda$.
$$\begin{align} \begin{pmatrix}x_{1} + \lambda x_{2} -x_{3}\\ y_{1} + \lambda y_{2} -y_{3} \\ z_{1} + \lambda z_{2} -z_{3} \end{pmatrix} \cdot \begin{pmatrix}x_{2} \\ y_{2} \\ z_{2} \end{pmatrix}=0 \end{align} $$

This will give some value for $\lambda$.

  1. Sub this value of $\lambda$ back into $\vec{d}$ to find the minimum distance vector.
$$\begin{align} \vec{d}=\begin{pmatrix}x_{1} + \lambda x_{2} -x_{3}\\ y_{1} + \lambda y_{2} -y_{3} \\ z_{1} + \lambda z_{2} -z_{3} \end{pmatrix}=\begin{pmatrix} a \\ b \\ c \end{pmatrix},\ a,b,c \in \mathbb{R} \end{align} $$
  1. Find the magnitude of $\vec{d}$.
$$\begin{align} \mid \vec{d}\mid = \sqrt{ a^{2}+b^{2}+c^{2} } \end{align} $$

This is the minimum distance between the centre of the sphere and the line, hence this represents the value of $\alpha$ that satisfies point 21.

From intuitive reasoning, it should be evident that point 12 is for values of $\alpha$ where $\alpha>\mid \vec{d}\mid$.

Likewise, point 33 is for values of $\alpha$ where $0<\alpha<\mid \vec{d}\mid$4

Enjoy this newfound knowledge!

Footnotes

  1. The sphere intersects the line once. ↩

  2. The sphere intersects the line twice. ↩

  3. The sphere does not intersect the line. ↩

  4. Notice the $0<\alpha$, this is very important! We can't have negative/null values for $\alpha$ as it represents a radius of a sphere. ↩