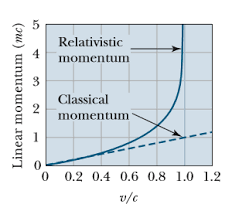
For particles moving at relativistic speeds,
$$\begin{align} p_{v}=\frac{m_{0}v}{\sqrt{1-\frac{v^2}{c^2} }} \end{align} $$$m_{0}$ is the rest mass. This is when you are measuring the mass within the same inertial frame of reference. In other words, when the particle is measured while it is at rest.
Note that as the Lorentz factor ($\frac{1}{\sqrt{ 1-\frac{v^2}{c^{2} }}}$) increases, the momentum of the particle increases a lot more than it would normally ($p=mv$)
Tempting to think that this implies mass changes with velocity.
At rest, $E=m_{0}c^2$. (Woah)
But, for a particle which we observe moving at relativistic speed, instead its total relativistic energy is represented as such:
$$\begin{align} E_{t}=\frac{m_{0}c^2}{\sqrt{ 1-\frac{v^2}{c^2} }} \end{align} $$Note that once again, $m_{0}$ represents the rest mass of the particle (same inertial frame of reference).
But then, what is the kinetic energy of the particle?
$$\begin{align} E_{t}&=E_{k}+E_{\text{rest}} \\ \therefore E_{k}&=E_{t}-E_{rest} \\ &= \frac{m_{0}c^2}{\sqrt{ 1-\frac{v^2}{c^2} }}-m_{0}c^2 \\ &=m_{0}c^2\left(\frac{1}{\sqrt{ 1-\frac{v^2}{c^2} }}-1\right) \end{align} $$This gives us the relativistic kinetic energy. DONT DO $\frac{1}{2}mv^2$!!!
Consider electron.
$$\begin{align} E_{\text{rest}}&=m_{0}c^2 \\ &=9.11 \times 10^{-31}\times 9 \times 10^{16} \\ &= 8.199 \times 10^{-14} \ J \\ &=0.512\ MeV \ (1\ MeV =1.6 \times 10^{-13} \ J) \end{align} $$Consider it is travelling at 0.9c.
Hence,
$$\begin{align} E_{t}&=\frac{m_{0}c^2}{\sqrt{ 1-\frac{v^2}{c^2} }} \\ &=\frac{9.11 \times 10^{-31}\times 9 \times 10^{16}}{\sqrt{ 1-0.9^2 }} \\ &=1.88 \times 10^{-13} \ J \\ \therefore E_{k}&=E_{t}-E_{\text{rest}} \\ &=1.88 \times 10^{-13}-8.199 \times 10^{-14} \\ &=1.06 \times 10^{-13}\ J \ \checkmark \end{align} $$