
The person outside the train sees the lightning strikes are simultaneous. But the person inside the train, because they're going closer to the right hand strike, the distance the light travels (remember, light travels at the same speed in all inertial frames of reference) is shorter, hence they see the right hand strike first, then the left hand one.
Thus, simultaneous events may not be simultaneous between inertial frames of reference.
Wait, so who is correct in their observation?!! Both of them are! Remember that the laws of physics are the same in all inertial frames of reference. Hence, there is no absolute frame of reference. Both frames are valid, and thus both observations are valid.
The proof: light clocky
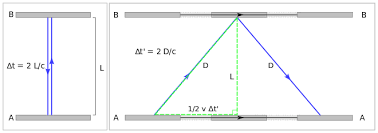
Consider a light clock moving relative to an observer A, and there's an observer B right moving along side the light clock (in the same inertial frame of reference).
Consider that light must be going at the same speed.
Hence, observer B sees the light from the light clock go straight up and straight down. It travels $2L$, i.e. the distance between the two ends of the light clock.
In contrast, because observer A sees the light clock moving, the light doesn't actually go straight up and straight down, instead, it moves sideways! In fact, it forms 2 right-angled triangles (up and down). It follows that the distance it travels is dependant on the velocity of the light clock, which provides the horizontal component of the right-angled triangle.
Hence, using Pythagoras,
$$\begin{align} D^2=L^2+\left( \frac{1}{2}vt \right)^2 \end{align} $$But $t=\frac{2D}{c}$, $t_{0}=\frac{2L}{c}.$ Hence,
$$\begin{align} D=\frac{tc}{2}, \ &L=\frac{t_{0}c}{2} \\ \therefore \left( \frac{tc}{2} \right)^2&=\left( \frac{t_{0}c}{2} \right)^2+\left( \frac{1}{2}vt \right)^2 \\ &\text{Rearranging for t:} \\ \frac{t^2c^2}{4}&=\frac{t_{0}^2c^2}{4}+\frac{v^2t^2}{4} \\ t^2c^2&=t_{0}^2c^2+v^2t^2 \\ t^{2} &= t_{0}^2+\frac{v^2}{c^2}t^2\\ t^2\left( 1+\frac{v^2}{c^2} \right)&=t_{0}^2 \\ t&=\sqrt{ \frac{t_{0}^2}{1+\frac{v^2}{c^2}} } \\ \therefore t&=\frac{t_{0}}{\sqrt{ 1+\frac{v^2}{c^2} }} \end{align} $$Where:
And if you check your formula sheet, this is the formula for time dilation!!!
The term $\frac{1}{\sqrt{ 1+\frac{v^2}{c^2} }}$ might look complicated, but luckily enough its the same thing for most of the relativity formulas. This is called the Lorentz or Gamma factor ($\gamma$).
$$\begin{align} \gamma=\frac{1}{\sqrt{ 1+\frac{v^2}{c^2} }} \end{align} $$Time to try this out!
Hence, we observe them moving slower.
Muons produced by cosmic radiation in upper atmosphere do not live long enough to reach Earth's surface but it turns out they do!
As they are travelling close to $c$, they experience time dilation
Hence, we observe them living longer than their mean life time from our frame of reference, however from their frame of reference, they are still living only up to their life time at rest.
Additionally, the distance it thinks it travels is much less compared to what we observe. This is because of length contraction!
This implies that the length that a separate observer sees an object travel is longer than what the object 'thinks' it travels.
Hence, we call $l_{o}$ the proper length, i.e. the length measured within the same inertial frame of reference for the moving object.
For example, say a 'rectangle' is thrown at 0.9c with a length of 15m at rest. Hence,
$$\begin{align} l &= l_{0}\sqrt{ 1-\frac{v^2}{c^2} } \\ &= 15 \times \sqrt{ 1-0.9^2 } \\ &=6.5m \end{align} $$What does this mean? Well, if I (me) was watching the rectangle pass by me, I would see it as 6.5m length wise. I.e. it becomes squishy!
https://faraday.physics.utoronto.ca/GeneralInterest/Harrison/SpecRel/Flash/Simultaneity.html